Summary: Explore the concept of determinants in mathematics, focusing on their application to non-square matrices. Learn about the challenges and insights th.. matrix; the matrix is invertible exactly when the determinant is non-zero. Properties Rather than start with a big formula, we’ll list the properties of the determi a b nant. We already know that = ad − bc; these properties will give us a c d formula for the determinant of square matrices of all sizes. 1. det I = 1 2.
Finding Determinant of a 2×2, 3×3,4×4 Matrix with Examples Teachoo
Determinant of Non Square 2 x 3 Matrix How to evaluate determinant of nonsquare 2 x 3 matrix
Evaluating the Determinant of a Matrix YouTube
Determinant of a Matrix with two Identical rows YouTube
![[Solved] Determinant of a nonsquare matrix](https://sgp1.digitaloceanspaces.com/ffh-space-01/9to5science/uploads/post/avatar/125030/template_determinant-of-a-non-square-matrix20220719-833071-1iy3hz4.jpg)
[Solved] Determinant of a nonsquare matrix 9to5Science
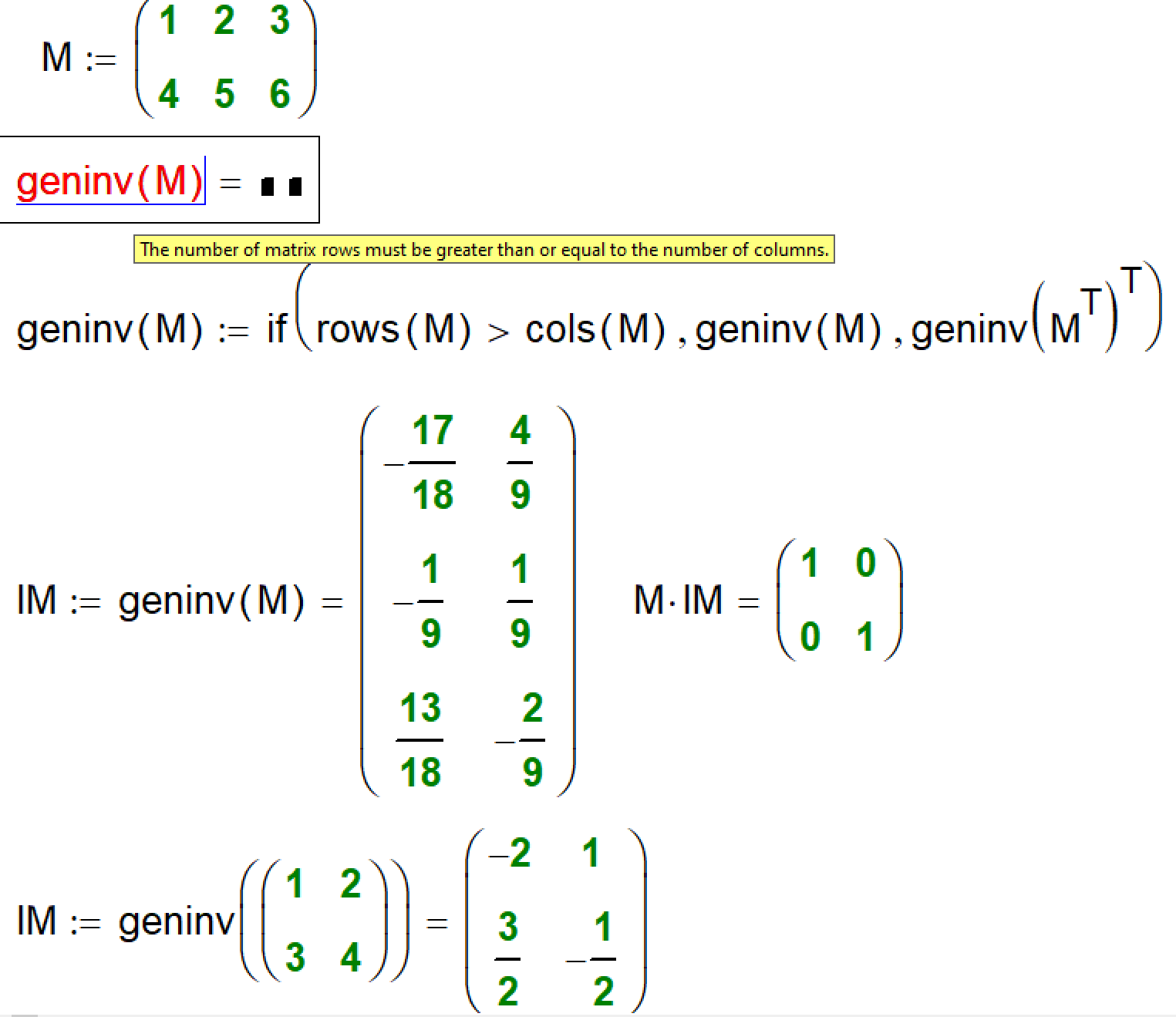
Solved Nonsquare matrix with left and right inverse matr… PTC Community
Determinant of a matrix
Matrices and Determinants Formula Sheet and Summary Teachoo
Determinant of a matrix Andrea Minini
Adjoint of a Square Matrix Definition, Theorem, Formulas, Solved Example Problems Inverse of
How To Find The Determinant of a 4×4 Matrix YouTube
PPT Square Matrix PowerPoint Presentation, free download ID4476765
Nonsquare matrices as transformations between dimensions Chapter 8, Essence of linear algebra
Adjoint and inverse of a square matrix W3schools
Determinant of a matrix pikollabel
How to Evaluate the Determinant of a 3×3 Matrix Quick & Easy Method YouTube
![[Determinants]Determinant of a n by n](https://i.ytimg.com/vi/sipjNpfpgrM/maxresdefault.jpg)
[Determinants]Determinant of a n by n matrix YouTube
PreCalculus 8.4 The Determinant of a Square Matrix part 2 YouTube
(PDF) DETERMINANT FOR NONSQUARE MATRICES
Mathematics Determinant of a nonsquare matrix (2 Solutions!!) YouTube
For large matrices, the determinant can be calculated using a method called expansion by minors. This involves expanding the determinant along one of the rows or columns and using the determinants of smaller matrices to find the determinant of the original matrix.. Theorem 3.2.1 3.2. 1: Switching Rows. Let A A be an n × n n × n matrix and let B B be a matrix which results from switching two rows of A. A. Then det(B) = − det(A). det ( B) = − det ( A). When we switch two rows of a matrix, the determinant is multiplied by −1 − 1. Consider the following example.
