Muestra cómo se pueden combinar varias técnicas e identidades para obtener una solución. Ejemplo 6.4.6: Using Trigonometric Substitution. Evaluar ∫ 1 ( x2 + 6x + 10)2 dx. Solución. Comenzamos completando el cuadrado, luego hacemos la sustitución u = x + 3, seguido de la sustitución trigonométrica de u = tanθ: ∫ 1 (x2 + 6x + 10)2 dx.. Aprende gratuitamente sobre matemáticas, arte, programación, economía, física, química, biología, medicina, finanzas, historia y más. Khan Academy es una organización sin fines de lucro, con la misión de proveer una educación gratuita de clase mundial, para cualquier persona en cualquier lugar.
Integración por sustitucion trigonométrica ∫(x^2 dx)/(x^2+8)^(3⁄2) YouTube
Integrales. Método de sustitución trigonométrica YouTube
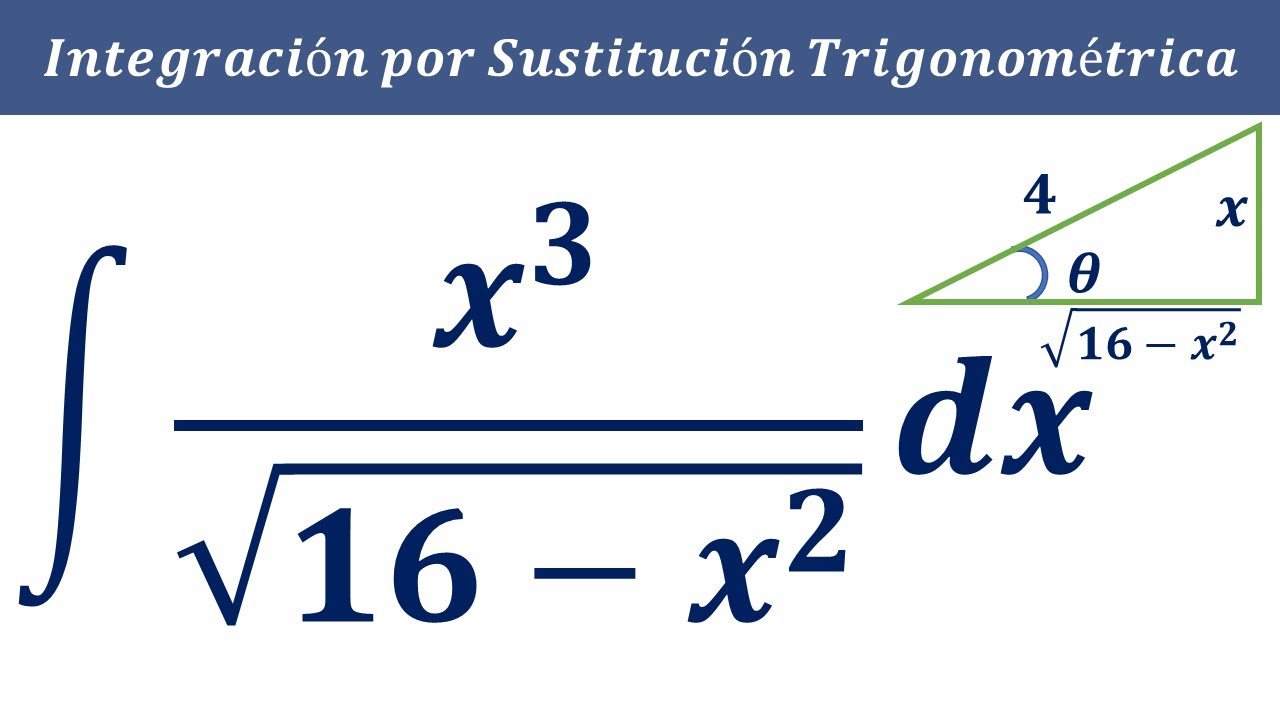
8 Integral Método de Sustitución Trigonométrica x^3 entre raíz 16x^2 dx Integración por
Integrales Método Sustitución Trigonométrica 1 Ejercicio 3 YouTube
.gif)
INTEGRALES POR SUSTITUCION TRIGONOMETRICA EJERCICIOS RESUELTOS PDF
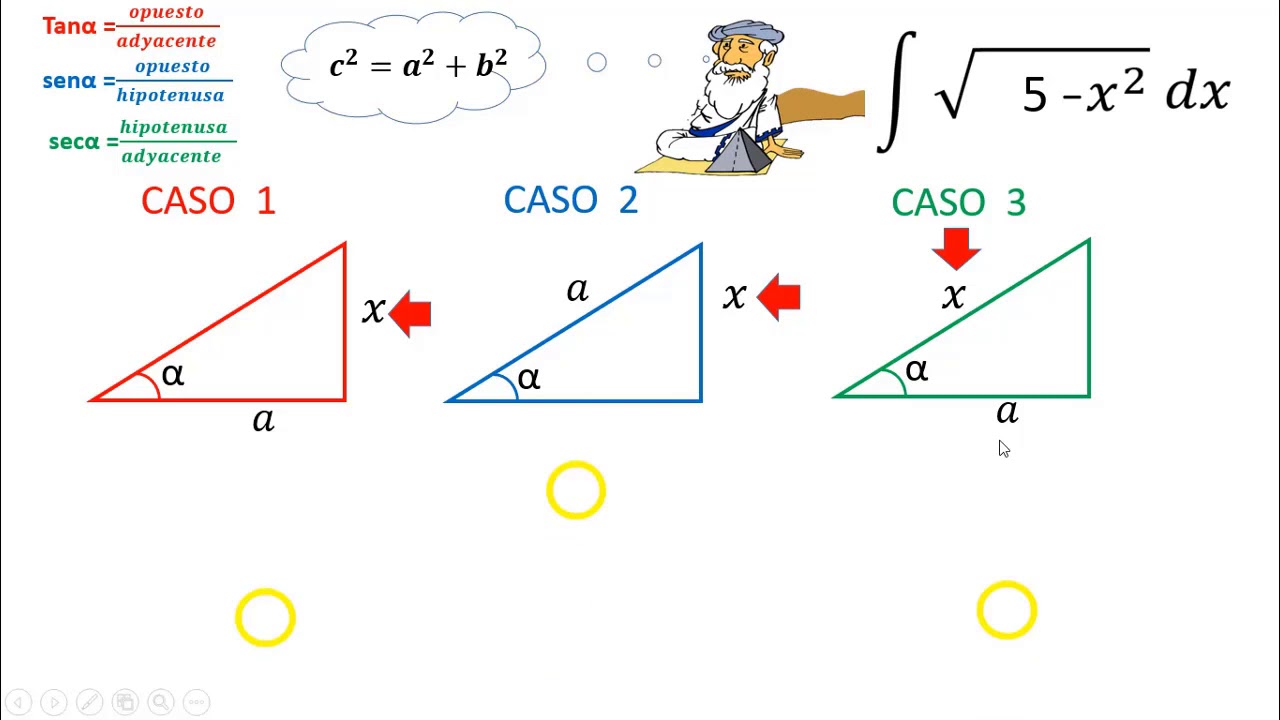
profe Daniel sustitución trigonométrica ” el triangulo” YouTube
Integrales por sustitución trigonométrica Ejemplo 1 YouTube
Integración por sustitución trigonométrica YouTube
.gif)
INTEGRALES POR SUSTITUCION TRIGONOMETRICA EJERCICIOS RESUELTOS PDF
¿Cómo y cuándo usar el método de Sustitución Trigonométrica? YouTube
Integración por sustitución trigonométrica. Ejemplo 2 YouTube
.gif)
INTEGRALES POR SUSTITUCION TRIGONOMETRICA EJERCICIOS RESUELTOS PDF
Integrales por sustitución trigonométrica YouTube
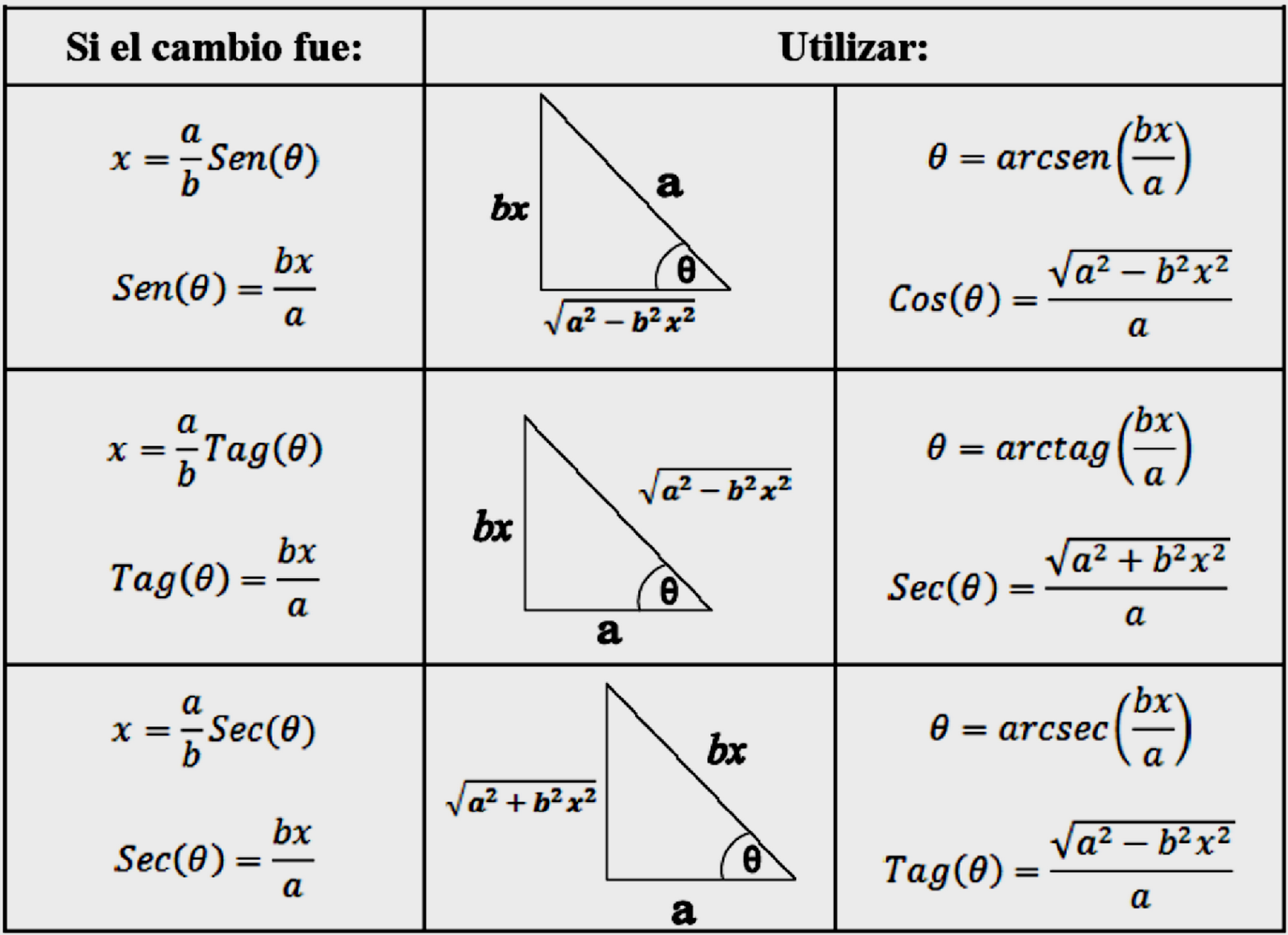
MÉTODO DE SUSUTICIÓN TRIGONOMÉTRICA
INTEGRACION POR SUSTITUCION TRIGONOMETRICA YouTube
7 Integración integrales por Método Sustitución Trigonométrica, raíz x^2 1 / x dx Como
Sustitución Trigonométrica. Caso I YouTube
Integración por sustitución trigonométrica YouTube
sustitucion trigonometrica 3 YouTube
MÉTODOS DE SUSTITUCIÓN TRIGONOMÉTRICA CASO I INTEGRALES 2020 03 30 1 YouTube
6.3: Sustituciones trigonométricas. Page ID. Michael Corral. Schoolcraft College. Una de las fórmulas fundamentales en geometría es para el área A de un círculo de radio r: A = πr2. La prueba basada en cálculo de esa fórmula utiliza una integral definida evaluada por medio de una sustitución trigonométrica, como se demostrará ahora.. 5.6 Técnica de sustitución trigonometrica. Se ejemplifica la técnica de sustitución trigonométrica para el cálculo de antiderivadas. En esta técnica de integración, la estrategia consiste en un cambio de variable utilizando alguna función trigonométrica que permite la reducción del integrando en algo que es una antiderivada inmediata.
